15 Convergence
15.1 Tail \sigma algebra
Let (\mathcal G_n) be a sequence of sub \sigma algebras of \mathcal H. Define the “future sigma algebra” containing events that depend only on the “tail” of the sequence beyond time n as
\mathcal T_n = \sigma \bigg( \cup_{m > n} \mathcal G_m \bigg)
Then the tail \sigma algebra is defined as:
\mathcal T = \cap_n \mathcal T_n
15.1.1 Example
Let X_1, X_2, \dots be random variables and \mathcal G_n = \sigma(X_n). Then \mathcal T contains events that depend only on the behaviour of X_n as n \to \infty.
For example,
- The event that X_n converges.
- The event that S_n = \sum_{i=1}^n X_i converges.
15.1.2 Kolmogorov’s 0-1 law
Let \mathcal G_1, \mathcal G_2, \dots be independent. Then, for any tail event A \in \mathcal T, \mathbb P(A) \in \{0, 1\}.
15.2 Almost sure
Let (\Omega, \mathcal H, \mathbb P) be a probability space. A sequence of random variables X_n converges almost surely if \mathbb P \{\lim\inf X_n(\omega) = \lim \sup X_n(\omega) \in \mathbb R\} = 1.
We say X_n \stackrel{a.s.}{\to} X if X_n converges almost surely and \lim X_n \stackrel{a.s.}{=} X.
\mathbb P( X(\omega) \lim X_n(\omega)) = 1
For general metric spaces, X_n \stackrel{a.s.}{\to} X \iff d(X_n, X) \stackrel{a.s.}{\to} 0.
An equivalent condition is: for any finite gap \varepsilon, only finitely many |X_n - X| exceed \varepsilon: X_n \stackrel{a.s.}{\to} X \iff \sum_n \mathbb 1[|X_n - X| > \varepsilon](\omega) \stackrel{a.s.}{<} \infty \forall \varepsilon > 0
15.2.1 Cauchy criterion
To check almost sure convergence without nowledge of the limit, there is an analogue of the Cauchy criterion. The following are equivalent:
- X_n converges almost surely
- \sup_{i, j \geq n} |X_i - X_j| \stackrel{a.s.}{\to} 0
- \sup_{k} |X_{n+k} - X_n| \stackrel{a.s.}{\to} 0
15.2.2 Continuous mapping theorem
Define f: \mathbb R^K \to \mathbb R, K \in \mathbb N. If
- X_{kn} \stackrel{a.s.}{\to} X_k for all k and
- f is continuous on a set A \subset \mathbb R^K such that \mathbb P((X_1, \dots, X_K) \in A) = 1 then f((X_{1n}, \dots, X_{Kn})) \stackrel{a.s.}{\to} f((X_{1}, \dots, X_{K}))
Note that the continuity set only needs to almost surely contain the limiting random vector, not the entire sequence.
15.2.3 Borel Cantelli theorem
Let (H_n) be a sequence of events.
\sum_n \mathbb P(H_n) < \infty \implies \sum_n \mathbb 1_{H_n}(\omega) \stackrel{a.s.}{<} \infty
Proof
By monotone convergence \infty > \sum_n \mathbb P(H_n) > \sum_n \mathbb E [\mathbb 1_{H_n}] = \mathbb E[\sum_n \mathbb 1_{H_n}]
And \mathbb E[X] < \infty \implies X \stackrel{a.s.}{<} \infty
15.2.4 Sufficient conditions
Using Borel-Cantelli and the characterisation we saw earlier (setting H_n = (\epsilon, \infty)) , we have a nice sufficient condition: \sum_n \mathbb P(|X_n - X| > \varepsilon) < \infty \forall \varepsilon > 0 \implies X_n \stackrel{a.s.}{\to} X
Alternatively, if we don’t know the limit in advance, we can use another sufficient condition:
There exists a sequence \varepsilon_n > 0 such that \sum_n \varepsilon_n< \infty and
\sum_n \mathbb P(|X_{n+1} - X_n| > \varepsilon_n) < \infty
15.3 In probability
X_n \stackrel{p}{\to} X if for all \varepsilon >0, \lim \mathbb P(|X_n - X| > \varepsilon) = 0
For general metric spaces, \lim \mathbb P(d(X_n, X) > \varepsilon) = 0
15.4 Uniform integrability
A family of random variables (X_t)_{t \in T} is uniformly integrable if
\lim_{b \to \infty} \sup_{t \in T} \mathbb E[|X_t| \mathbb 1(|X_t| > b)] = 0
Theorem 15.1 Uniform integrability implies that there is a uniform bound on the expectation۔ of X_t i.e. \sup_{t\in T} \mathbb E[|X_t|] < \infty. The converse is not true in general.
Theorem 15.2 If the p-norm is bounded i.e., \sup_{t \in T} \mathbb E[|X_t|^p] < c < \infty for some p > 1 then the sequence (X_t)_{t \in T} is uniformly integrable.
Proof
\begin{align*} \mathbb E[|X_t|] &= \mathbb E[|X_t| 1_{|X_t| \leq b}] + \mathbb E[|X_t| \mathbb 1_{|X_t| > b}]\\ &\leq \mathbb E[|X_t| \mathbb 1_{|X_t| \leq b}] + b\\ \end{align*}
Fix \epsilon>0, since the limit of the first term is zero, we can find a finite B such that for all b > B, \sup_{t \in T} \mathbb E[|X_t| \mathbb 1_{|X_t| > b}] < \epsilon
and thus \sup_{t \in T} \mathbb E[|X_t|] \leq \epsilon + B +1< \infty.A family of random variables (X_t)_{t \in T} is uniformly integrable if and only if there exists a convex function \phi: \mathbb R_+ \to \mathbb R_+ such that \lim_{x \to \infty} \frac{\phi(x)}{x} = \infty and \sup_{t \in T} \mathbb E[\phi(|X_t|)] < \infty.
15.4.1 Example
If X \in L^1 then the collection \{\mathbb E[X| \sigma \mathcal G] : \sigma\mathcal G:\mathcal G \subseteq \mathcal F\} is uniformly integrable.
15.5 L^p convergence
\mathbb E[|X_n - X|^p] \to 0
15.5.1 L^1 convergence
The following are equivalent:
- X_n \stackrel{L^1}{\to} X
- X_n \stackrel{p}{\to} X and (X_n) is uniformly integrable
- X_n \in L^1, X \in L^1, X_n \stackrel{p}{\to} X and \mathbb E|X_n| \to \mathbb E|X|
If integrable X_n \stackrel{L^1}{\to}X then \mathbb E[X_n 1_A] \to \mathbb E[X 1_A]
Theorem 15.3 (Cauchy criterion) Let (X_n) be a sequence of real valued random variables
Then it converges in L^1 iff
\lim_{k} \sup_{m,n \geq k} \mathbb E|X_n - Xm|= 0
15.6 Weak convergence
15.6.1 Definition
A sequence of measures converges weakly \mu_n \stackrel{w}{\to} \mu if for every bounded continuous function f:
\mu_n[f] \to \mu[f]
For convergence in distribution of a sequence of random variable X_n \stackrel{d}{\to} X, we require convergence of the pushforwards \mathbb P \circ X_n^{-1} i.e. for every bounded continuous function f: \mathbb[f(X_n)] \to \mathbb E [f(X)]
15.6.2 Portmanteau theorem
The following are equivalent:
- \mu_n \stackrel{\to}{w} \mu
- \lim \sup \mu_n(A) \leq \mu(A) for every closed set A
- \lim \inf \mu_n(A) \leq \mu(A) for every open set A
- \lim \mu_n(A) = \mu(A) for every Borel set with \mu(\partial A) = 0
15.6.3 Continuous mapping theorem
Proof
In this new space, \mathbb P(Y \in D_h) =\mathbb P(X \in D_h) = 0 i.e. the set of discontinuity points is negligible. Thus, for all \omega in the complement,
Y_n \stackrel{a.s.}{\to} Y \implies h(Y_n) \stackrel{a.s.}{\to} h(Y)
And since there exists a probability space where this almost sure convergence holds, and in our original space we have h(X_n)= h(Y_n) and h(X)= h(Y), thus again by Skorokhod’s representation theorem, we can conclude h(X_n) \stackrel{d}{\to} h(X).
15.6.4 Uniqueness
If \mu_n \stackrel{w}{\to} \mu and \mu_n \stackrel{w}{\to} \nu then \mu = \nu.
15.6.5 Prokhorov’s theorem
If (\mu_n) is tight, then every subsequence has a further subsubsequence that converges weakly.
In practice, if we can show:
- Any subsequence of \mu_n has a subsubsequence that converges weakly.
- The weak limit is the same for each subsubsequence, say \mu.
Then, for any bounded continuous f, each subsequence of \mu_n f has a subsubsequence converging to \mu f, and thus \mu_n f \to \mu f \implies \mu_n \stackrel{\to}{w} \mu.
We use Prokhorov’s theorem to show (1) - the condition required is tightness i.e. for every \epsilon > 0 there exists a compact set K such that for all n, \mu_n(K) > 1- \epsilon
15.6.6 Levy’s convergence theorem
Let f_n(r) = \int \exp(irx) \mu_n(dx). \mu_n is weakly convergent if and only if the pointwise limit f(r) = \lim f_n(r) exists, and the function f is continuous at 0. In this situation, \mu_n \stackrel{w}{\to} \mu where:
f(r) = \int \exp(irx) \mu(dx)
15.7 Relations
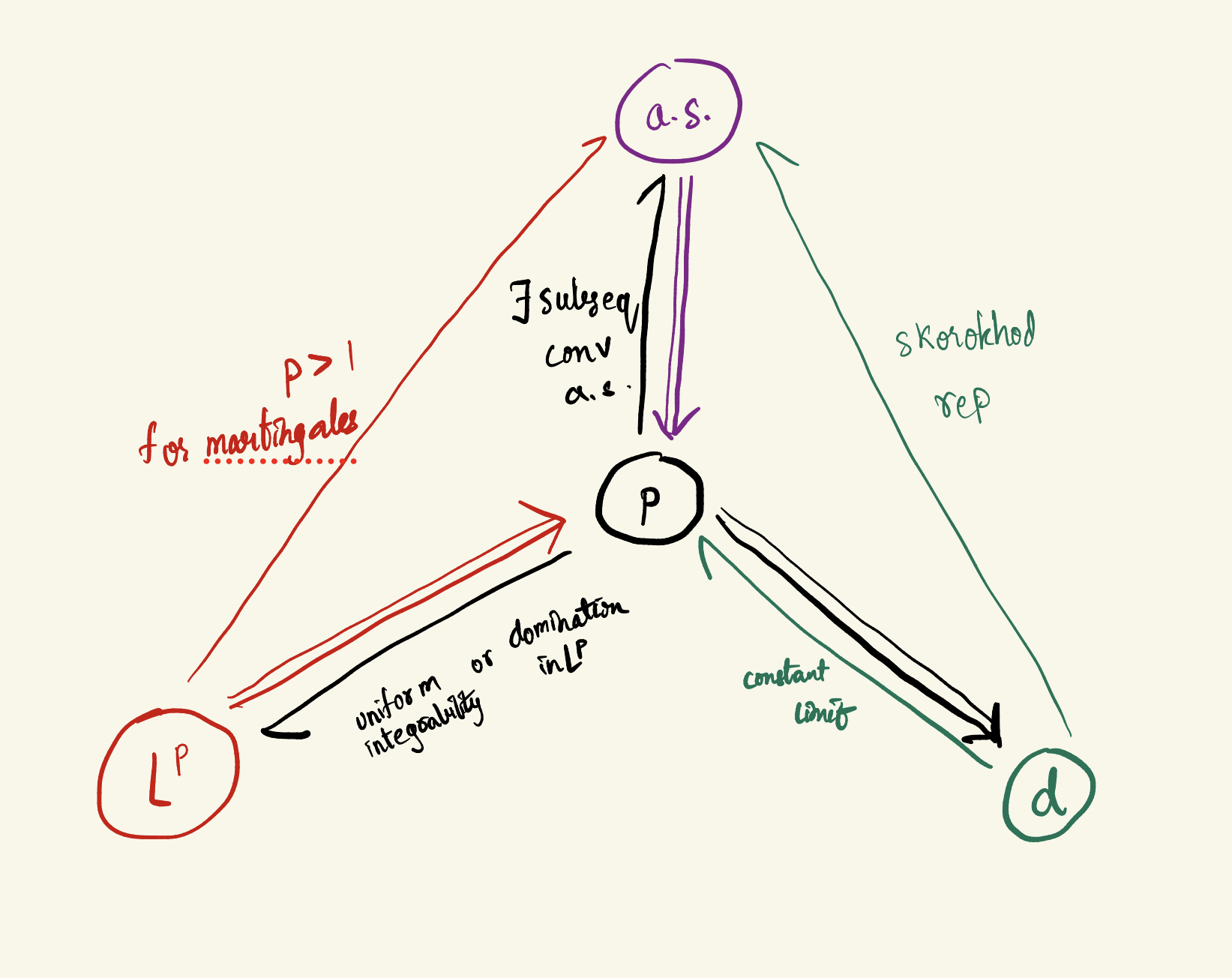
15.7.1 Vitali convergence theorem
The following are equivalent: 1. X_n \stackrel{L^1}{\to} X 2. X_n \stackrel{p}{\to} X and (X_n) is uniformly integrable
More generally, for p \geq 1, the following are equivalent: 1. X_n \stackrel{L^p}{\to} X 2. X_n \stackrel{p}{\to} X and (|X_n|^p) is uniformly integrable
15.7.2 Relation of almost sure convergence and convergence in probability
- X_n \stackrel{a.s.}{\to} X \implies X_n \stackrel{p}{\to} X
Proof
X_n \stackrel{a.s.}{\to} X implies for all \varepsilon > 0:
\sum_n \mathbb 1[|X_n - X| > \varepsilon](\omega) \stackrel{a.s.}{<} \infty
and thus
\mathbb 1[|X_n - X| > \varepsilon](\omega) \stackrel{a.s.}{\to} 0
Now, for \varepsilon > 0
\begin{align*} \lim \mathbb P(|X_n - X| > \varepsilon) &= \lim \mathbb E \mathbb 1[|X_n - X| > \varepsilon]\\ &= \mathbb E \lim \mathbb 1[|X_n - X| > \varepsilon] \text{by dominated convergence using 1}\\ &= 0 \end{align*}
If X_n \stackrel{p}{\to} X then there exists a subsequence (n_i) such that X_{n_i} \stackrel{a.s.}{\to} X
If every subsequence of X_n has a further subsequence that converges to X almost surely then X_n \stackrel{p}{\to} X
15.7.3 Convergence in L^p implies convergence in probability
Proof
For every \varepsilon>0:
\begin{align*} \lim \mathbb P(|X_n - X| > \varepsilon) &= \lim \mathbb P(|X_n - X|^p > \varepsilon^p)\\ &\leq \lim \frac{|X_n - X|}{\varepsilon^p} \text{Markov's inequality} &= 0 \end{align*}
15.7.4 Convergence in probability implies weak convergence
Proof
Assume X_n \stackrel{p}{\to} X. Then, for every subsequence (n_i) there exists a subsubsequence (n_{i_j}) such that X_{n_{i_j}} \stackrel{a.s.}{\to} X.
Here,
\begin{align*} \lim X_{n_{i_j}}(\omega) &\stackrel{a.s.}{=} X(\omega) \\ \lim f(X_{n_{i_j}}) &= f(\lim f(X_{n_{i_j}})) \quad \text{continuity of $f$}\\ &\stackrel{a.s.}{=} f(X(\omega)) \\ \lim \mathbb E[ f \circ X_{n_{i_j}} ] &= \mathbb E[\lim f(X_{n_{i_j}})] \quad \text{DCT, boundedness of $f$}\\ &= \mathbb E [f \circ X] \end{align*}
Thus every subsequence of \mathbb E[f \circ X_n] has a subsubsequence that converges to \mathbb E[f \circ X] so \mathbb E[f \circ X_n] \to \mathbb E [f \circ X] thus X_n \stackrel{d}{\to} X
15.7.5 Skorokhod representation
Let (\Omega, \mathcal H, \mathbb P) be our probability space, with random variables (X_n) and X. Then X_n \stackrel{d}{\to} X if and only if there exists another probability space (\Omega', \mathcal H', \mathbb P') and random variables on that space (Y_n) and Y such that
X_n \stackrel{d}{=} Y_n X \stackrel{d}{=} Y Y_n \stackrel{a.s.}{\to} Y